Cosmic Acoustics Part 2

In Cosmic Acoustics Part 1, we discussed acoustics on the scale of the observable universe. We look at the makeup of our early universe and studied it like we study sound here on earth. We determined approximately how loud (in decibels) the early universe was based on the Cosmic Microwave Background (CMB). Today, we will take another look at the early universe to see what other characteristics of sound we can find hidden in it.

Did the Early Universe Strike a Chord?

Here on earth, we can measure the frequency of sound waves by counting how much time passes between wave peaks. For example, we can measure a 60 Hz tone will produce pressure peaks roughly once every 0.017 seconds, or 60 peaks in one second.

Last time we left off with this plot of a Fourier transform: displaying the pitches emitted by a flute. Shown are the relative loudnesses of each frequency (in kiloHertz, or kHz). To put units in perspective, 1 kHz = 1,000 Hz, or 1,000 sound wave peaks passing by per second. The physical design of a flute emphasizes certain frequencies and dedicates much more acoustic energy into exciting them. These frequencies often start with the strongest fundamental (lowest) frequency, as shown all the way on the left of the plot at 262 Hz, or C4. Then come added harmonics which are integer multiples of the fundamental frequency.

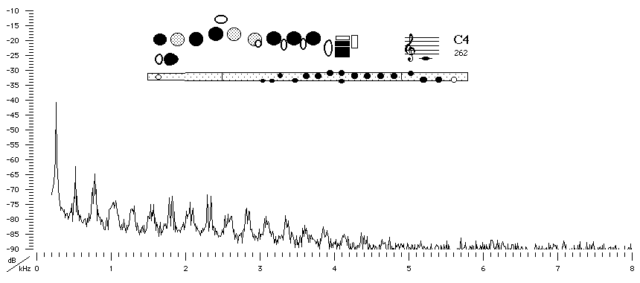
Note that the y-axis in this image is measured in decibels. The fundamental frequency plays the loudest with successive harmonics tapering off in relative loudness. Now that we understand the frequency content of a flute tone, we can look at our early universe in a similar manner.

Due to the immense cosmic size of the early universe, we cannot simply measure the time between wave peaks in the cosmic microwave background. The time between peaks (period) of primordial acoustic waves is somewhere between 20,000 to 200,000 years! Since the CMB was only discovered in 1964, we need to find a different way to measure wave frequency.

What we can measure is wavelength instead of period. Going further, instead of measuring regular old Cartesian wavelengths in feet or meters, we can ask ourselves what angle (e.g. how many degrees) of the sky does one wavelength take up? Knowing this, and the fact that the speed of sound back then was similar to the speed of light due to the abundance of photons pushing everything around, we can calculate the angular frequency of these primordial acoustic waves (also called the multipole moment). The angular frequency is roughly 180 divided by the wavelength in degrees. So, when we run a Fourier method to extract the relative loudness of each angular frequency over the entire cosmic microwave background, we see the following.

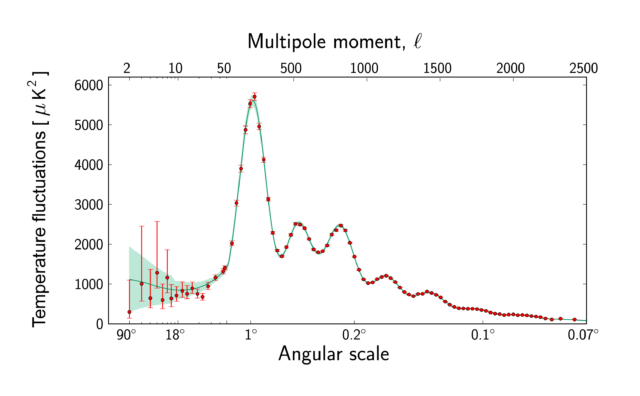
The y-axis here is in microkelvin, the same units governing the color scale of NASA’s WMAP CMB snapshot discussed in Cosmic Acoustic Part 1, with additional correction factors to adjust for the 2D nature of the sky’s plane. Using our same approximation we used to determine the overall sound level of these primordial waves (that temperature is proportional to pressure), we can see a spectral plot very similar to that of a C4 played on a flute. The top axis (multipole moment) is analogous to frequency as in our flute plot, and the bottom axis (angular scale) is analogous to wavelength. There appears to be a fundamental frequency with a few harmonics tapering off in magnitude, just like we saw in the spectral decomposition of a C4 played on the flute.

So what might this early universe set of harmonics sound like? There are plenty of simulations out there that attempt to sonify the early universe. They do so by converting angular frequency of the sky to regular, human-friendly, frequency measured in Hertz. By raising the pitch of these CMB acoustic wave signatures up 50 or so octaves to the human hearing range, we can listen to an earth-friendly rendition of the origins of creation. Some even change in pitch to account for the inflation of the universe over time.

On the Origin of Sound

Is anyone else curious about the seemingly random appearance of acoustic harmonics in the cosmic microwave background? “Why is the same thing I hear a flute play appearing in the earliest days of our universe?” Flute tones and overtones stem from the constrained nature of the instrument. Hard metal boundaries create zones of minimal and maximal pressure inside the flute and amplifies frequencies whose wavelengths correspond to this pressure distribution. If our universe were unconstrained and unbounded, where would tones and overtones come from? Let us explore why these acoustic waves might have appeared in the first place.

As we said before, the universe started out relatively uniform. No differences in density, temperature, or pressure anywhere. Physicists believe that after one Planck second (10^(-43) seconds, the shortest duration where time has any meaning) the laws of quantum mechanics as we know it started to turn on and tiny fluctuations in position bubbled up due to the uncertainty principle. These teensy-tiny perturbations caused teensy-tiny differences in density in the early universe. Once there was an initial non-uniformity in the universe, things began to evolve. Space becomes filled with randomly distributed clumps of matter.

Matter and gravity are intertwined. These dense matter-pockets of the nearly-uniform universe had gravity, and so our fledgling elementary particles, hot ionized gas (hydrogen and helium), and rogue electrons whizzing through the universal fog all began to fall into these gravity wells(aka potential wells). Sometimes the matter jumped in with too much energy and would be ejected, sling-shot style, back into the more-uniform regions of the universe on the other side of these matter-pockets. This created a universe full of gasses jumping in and out of gravity wells, causing roughly radial pulsations of matter around each of these matter-clumps. When gas molecules gather in the bottom of one of these gravity wells, this is called compression. When gas molecules rebounded into the more-uniform parts of the universe, this is called rarefaction. These phenomena of compression and rarefaction are fundamental to the study of sound on earth.

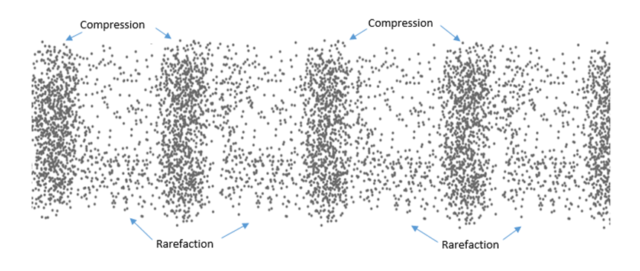
These compression zone matter-clumps grew throughout the universe, some growing larger than others did. The larger the matter clump, the longer it took for the surrounding gas to fall into and jump back out of their grasp. Compression occurred most effectively when matter fell into any gravity well for the very first time when it had little to no energy.  Because the cosmic microwave background is essentially the yearbook photo of our 400,000-year-old universe, what we see as the fundamental tone in the angular power spectrum arises from the simultaneous initial compression of gas in the largest existing matter pockets. The fundamental is seen in the amount of gas compressing and rarefying at maximum efficiency at the exact moment recombination took hold and cleared out our universe.

Given the 400,000 years these compression waves had to do their thing, and given the fact that the speed of sound at this time was close to the speed of light, some number crunching can be done to determine that the fundamental tone of the cosmic microwave background had a wavelength around 220,000 light-years long. This equates to a frequency of roughly one ten-trillionth of a hertz!

Universal Harmony

The existence of a fundamental frequency in the cosmic microwave background does not arise in quite the same way as a fundamental arises for a flute. The same is true with harmonics. Odd harmonics in the CMB arise from other, smaller matter clumps sucking in and spewing out ionized gas in time with the largest gravity wells at 400,000 years. These smaller clumps that had pulled in the surrounding gas two, three, maybe four times in 400,000 years, and when the snapshot was taken, they happened to have a lot of gas particles around them, causing a compression peak.

Even harmonics in the CMB arise from smaller matter clumps whose gaseous oscillations were 180 degrees out of phase with the large fundamental clumps. These clumps had just shot all surrounding gas out into the more-uniform universe, causing a rarefaction peak in the CMB spectrum.

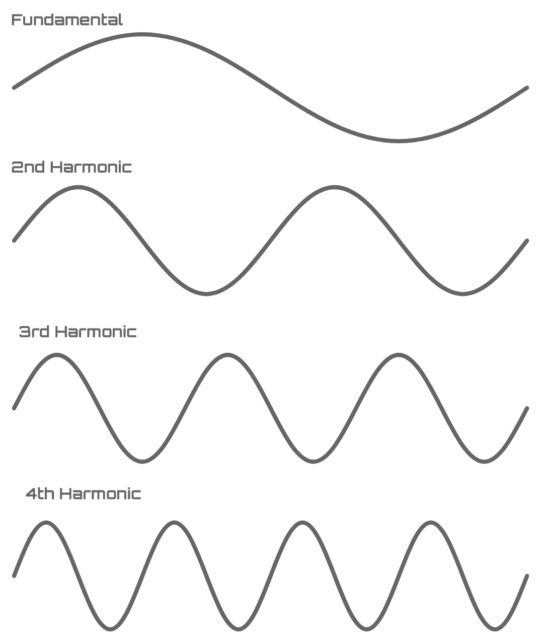
There were certainly matter-clumps whose compression-rarefaction schedules were not so nicely aligned with the fundamental captured in the CMB. These matter clumps with gas in an intermediate state between fully compressed and fully rarefied appear as frequencies that lie between the fundamental and harmonic frequencies. They add to the wideness of each tonal peak and blur the exact frequencies that are in harmony with one another.

What Does It All Mean?

We have come a long way from Ridley Scott’s Alien and the bumper car analogy for sound waves propagating through a medium discussed in Part 1. What can we take away from our learnings so far?

Well, as architectural acousticians on earth, once we know the sound pressure level and frequency spectrum of a sound source, we can tell a lot about the structure and composition of the room our source is in. We can use our measurements to help us determine the room dimensions and shape, types and amount of finishes and even the directional characteristics of the sound source itself. As laid out in Parts 1 and 2 of this blog, we have a very similar set of information about the early universe.

By looking at tones and spectra present in the acoustic waves of the early universe, we can begin to understand its structure and composition. Two major fields of research involving primordial acoustic waves include understanding the density of the universe, and the distribution of matter in the universe. By looking at the relative strength of the fundamental to each successive harmonic, we can learn about the presence of dark matter and dark energy in our universe. By matching various models to multiple data sets of CMB information, we can create a model of the early universe that most accurately matches our measurements of the CMB. Some of the most accurate models we have made predict that at the time of recombination, regular old baryonic matter (anything made of atoms, protons, neutrons, electrons, etc.) only made up a small percent of our universe. The majority of our universe is made up of mysterious dark energy and dark matter.

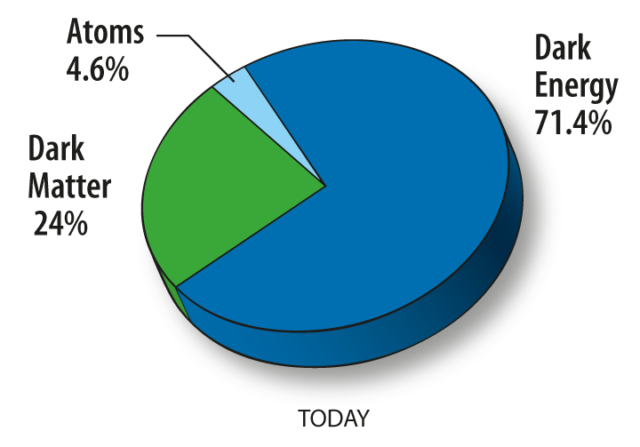
We cannot say much about dark matter and dark energy because we have never directly observed them; however, we begin to see the influence of dark matter and dark energy have on the universe we live in. Thus, we are beginning the scratch the surface of entirely new fields of study simply by understanding that acoustic waves once propagated throughout the universe.

While our ears may not pick up distress calls from alien attacks in space, we now know there is a time and a place for acoustics in space.